
Didattica della Matematica Inclusiva
nella scuola secondaria di primo grado
ATTIVITÀ 2
Si riportano alcuni spunti possibili per lanciare la discussione in classe sul secondo aspetto che vogliamo trattare in questa fase: “quanto andrò avanti con l’algoritmo in Q?”
Come già osservato, la discussione potrebbe nascere proprio a partire dai dubbi degli studenti; anzi, si aprirà un dibattito ancora più acceso in classe se l’esigenza di conoscere e di capire cosa accade viene dagli studenti stessi.
Per esempio, nel dialogo mostrato nell’immagine di seguito, uno studente si chiede se svolgendo l’operazione con la calcolatrice avrebbe trovato più cifre decimali (forse infinite) del quoziente. In altre parole, se la divisione di due numeri interi può dare origine ad un numero irrazionale.
Gli studenti di questa classe sperimentale erano abituati alla scuola primaria a fermarsi alla terza cifra decimale del quoziente (quindi spesso il quoziente da loro trovato non corrispondeva al risultato della calcolatrice). Il compagno toglie il dubbio spiegandogli che avendo ottenuto resto zero può star sicuro che la divisione è finita.

Esempio di dubbio e relativa discussione in una classe sperimentale.
Indicazioni per il docente
L’insegnante valorizza il dubbio di alcuni studenti che si domandano se potrà mai succedere di andare avanti all’infinito con l’algoritmo di divisione, trovando nel quoziente infinite cifre decimali sempre diverse (ovvero un numero decimale illimitato non periodico). Nel caso in cui la questione non dovesse emergere spontaneamente, può essere proposta come domanda aperta dall’insegnante stesso.
La discussione di classe si pone i seguenti obiettivi:
-
superare le comuni “regole” fornite spesso alla scuola primaria che definiscono dei criteri per interrompere l’algoritmo (ad esempio aggiungere solo 3 zeri dopo la virgola, ovvero fermarsi alla terza cifra decimale del quoziente);
-
prendere consapevolezza che il numero di resti possibili che si possono ottenere non è infinito: sono tutti i numeri naturali da 0 a n-1, con n=divisore;
-
realizzare che l’algoritmo di divisione necessariamente si fermerà (resto zero) o andrà “in loop” (portando quindi alla ripetizione di un insieme di cifre decimali, dette periodo);
-
comprendere che il quoziente tra due numeri interi sarà necessariamente un numero razionale.
Cosa aspettarsi
Durante l’esplorazione dell’algoritmo canadese e della sua logica di svuotamento progressivo del dividendo attraverso multipli del divisore, gli studenti iniziano a prendere consapevolezza che i possibili resti della divisione in N non sono infiniti. Osservano che il resto deve essere necessariamente un numero minore del divisore. Se infatti il resto fosse uguale o maggiore del divisore, sarebbe possibile procedere con un’altra sottrazione. Questa presa di consapevolezza è importantissima per l’obiettivo che ci poniamo in questa fase.
Per esempio, uno studente di una delle classi sperimentali ha osservato, molto entusiasta della sua scoperta, probabilmente inaspettata dal tono della voce:
“Prof, ma quindi non ci sono tante possibilità, il resto [nella divisione 222 : 8] è per forza, cioè non è che posso trovare qualsiasi numero. So che deve essere per forza più piccolo di 8, cioè… o 1 o 2 o 3 o 4 o 5 o 6 o 7 sennò non c’è proprio” “…e quindi se la divisione fosse per 2, il resto potrebbe essere solo 1, oppure non c’è.”
Una divisione che è stata utilizzata nelle classi sperimentali per riflettere su questo aspetto è 6 : 7.
Osserviamo che queste attività si possono inserire nella Fase 4 del percorso sulle frazioni in cui si discute la relazione tra frazione e numero decimale operando una sorta di classificazione delle frazioni in ragione del tipo di numero che genera la divisione.
La divisione 6 : 7 è un buon esempio perché ha come quoziente un numero periodico con periodo di 6 cifre. Si può iniziare a farla svolgere alla lavagna da uno studente e, dopo qualche passaggio, chiedere alla classe cosa si aspetta possa succedere.
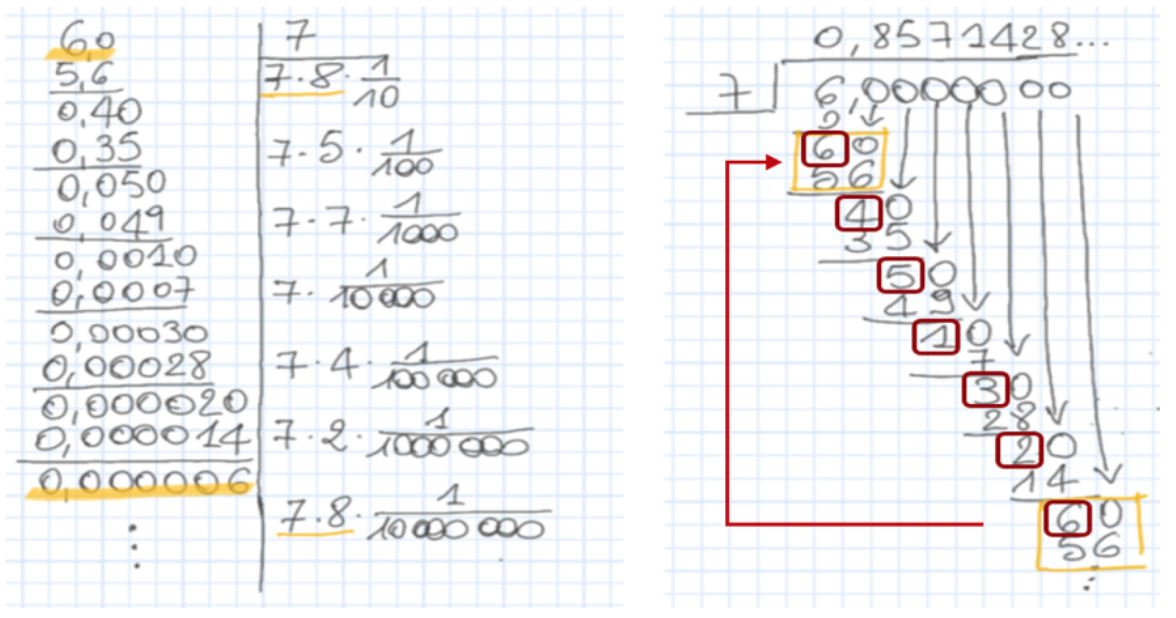
La discussione in classe porta gli studenti a rendersi conto che i possibili resti sono solo i numeri da 0 a 6. Se si trova resto 0, la divisione finisce, altrimenti una volta trovati tutti gli altri possibili resti (1, 2, 3, 4 e 5), dovranno per forza ripetersi. A quel punto anche l’algoritmo non potrà che ripetersi uguale a se stesso infinite volte dando origine, come quoziente, ad un numero decimale illimitato ma periodico.
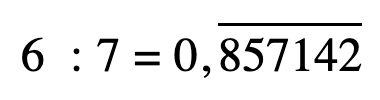
Inoltre, per tornare su questo in un secondo momento si può chiedere agli studenti se il risultato dell’operazione 120 : 17 sia o meno un numero razionale. Molti studenti sono portati a non usare l’evidenza teorica discussa in classe, che ha bisogno di tempo per sedimentare in loro, ma a svolgere la divisione attraverso l’uso della calcolatrice o manualmente con uno degli algoritmi imparati.
L’operazione è particolarmente fastidiosa perché il suo risultato è un numero periodico con periodo di 16 cifre che va oltre le normali posizioni contenute nel display di una calcolatrice. A prima vista potrebbe quindi sembrare un numero irrazionale. Solo la pazienza di qualche studente volenteroso nel portare avanti un algoritmo parecchio lungo piuttosto che l’uso invece di una argomentazione teorica convincente (i possibili resti sono da 0 a 16) potranno risolvere i dubbi e convincere tutta la classe che il risultato deve essere un numero razionale. Un ultimo controllo potrà poi essere effettuato tramite l’uso della calcolatrice del pc.

Vai alle Conclusioni della Fase 2 ➜
2018_3_1011_IP.01 “LE NUOVE FRONTIERE DEL DIRITTO ALL’ISTRUZIONE. Rimuovere le difficoltà d’apprendimento, favorire una scuola inclusiva e preparare i cittadini responsabili e attivi del futuro - Fase 2". Questa iniziativa è realizzata nell'ambito del Programma operativo FSE 2014 – 2020 della Provincia autonoma di Trento grazie al sostegno finanziario del Fondo sociale europeo, dello Stato italiano e della Provincia autonoma di Trento. La Commissione europea e la Provincia autonoma di Trento declinano ogni responsabilità sull’uso che potrà essere fatto delle informazioni contenute nei presenti materiali.

