
Didattica della Matematica Inclusiva
nella scuola secondaria di primo grado
FRAZIONI SUL FILO > FASE 1 > ATTIVITÀ 1 > ATTIVITÀ 2
ATTIVITÀ 2
Per verificare se quanto discusso nella prima consegna è stato veramente interiorizzato, si invitano gli studenti a replicare il lavoro svolto con i fogli A4 sul quaderno, utilizzando un rettangolo 6x12 quadretti.
Si chiede loro di realizzare le unità frazionarie 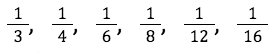 in almeno due modi diversi.
in almeno due modi diversi.
Questa attività può essere svolta in classe, lasciando lavorare gli studenti individualmente.
Si consiglia all’insegnante di scansionare tutte le produzioni dei propri studenti in modo da raccoglierle poi in alcune slide per la lezione successiva. La presentazione permette di rilanciare la discussione in classe, attraverso cui arricchirsi delle varie idee dei compagni e comprendere eventuali errori tramite il confronto.
Cosa aspettarsi
Riportiamo la foto del quaderno di due studenti molto ordinati. Pur avendo lavorato entrambi in modo corretto, si noti come lo studente a sinistra sia rimasto legato alla divisione in parti congruenti, mentre la studentessa a destra in alcune tovagliette sembra aver abbandonato il concetto di forma per considerare l’equiestensione.

Di seguito riportiamo anche alcune slide che sono state usate nelle classi sperimentali per la discussione della lezione successiva, in cui si confrontano diverse realizzazioni di ciascuna unità frazionaria.



È importante chiedere agli studenti di spiegare la strategia utilizzata per ottenere le varie unità frazionarie. In particolare possono dare molto fastidio, e quindi dar luogo a discussioni interessanti, le realizzazioni con forme “strane”. Gli studenti che realizzano tovagliette con forme originali hanno capito che, una volta noto il numero di quadretti di ciascuna unità frazionaria, si può dar libero sfogo alla fantasia! Gli studenti più deboli, invece, tendono a non sentirsi pronti per tutta questa libertà e spesso rimangono ancorati a forme più “standard”, ma è importante che capiscano la correttezza anche delle realizzazioni dei compagni.

Inoltre proponiamo alcuni esempi di errori comuni, che è interessante discutere in classe perché è il confronto tra pari ad aiutare questi studenti a capire cosa hanno sbagliato.
Le unità frazionarie che solitamente danno origine a diversi errori sono 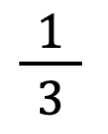 e
e 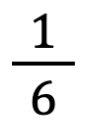 , ma quella più complicata, perché richiede di considerare metà quadretto, è
, ma quella più complicata, perché richiede di considerare metà quadretto, è 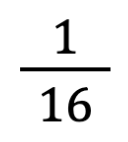 .
.

Infine, osserviamo che durante l’attività di costruzione di questa pagina di quaderno gli studenti sviluppano spontaneamente ragionamenti di confronto e ordinamento delle unità frazionarie. In particolare, si accorgono del legame tra una frazione e la sua metà (ad esempio che è metà di
) e della relazione che sussiste tra l’ordinamento delle unità frazionarie e la grandezza del denominatore. Si potrebbe ritenere questo aspetto banale per studenti di scuola secondaria ma non sempre è così: il numero “più grande” al denominatore induce spesso in errore. Il potenziale di queste attività è che aiutano a costruirsi immagini mentali che poi gli studenti possono richiamare nei loro ragionamenti e usare come strumenti di pensiero.


Se non dovesse emergere in modo spontaneo dagli studenti, l’insegnante può chiedere loro di confrontare alcune unità frazionarie che hanno un rapporto facile come e
oppure
 e
e  ma anche
ma anche e
 . Questo poi torna utile per disegnare unità frazionarie tipo
. Questo poi torna utile per disegnare unità frazionarie tipo  , come metà di
, come metà di . Gli studenti che colgono questi rapporti spesso proseguono a disegnare anche
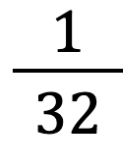 ,
, 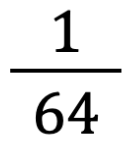 …
…
2018_3_1011_IP.01 “LE NUOVE FRONTIERE DEL DIRITTO ALL’ISTRUZIONE. Rimuovere le difficoltà d’apprendimento, favorire una scuola inclusiva e preparare i cittadini responsabili e attivi del futuro - Fase 2". Questa iniziativa è realizzata nell'ambito del Programma operativo FSE 2014 – 2020 della Provincia autonoma di Trento grazie al sostegno finanziario del Fondo sociale europeo, dello Stato italiano e della Provincia autonoma di Trento. La Commissione europea e la Provincia autonoma di Trento declinano ogni responsabilità sull’uso che potrà essere fatto delle informazioni contenute nei presenti materiali.

