FRAZIONI SUL FILO > FASE 3 > ATTIVITÀ 1 > ATTIVITÀ 2 > PROPOSTE DI CONSOLIDAMENTO > ATTIVITÀ 3

 

ATTIVITÀ 3

Nelle prime due attività le frazioni sono posizionate sulla retta dei numeri disegnata sul quaderno degli studenti e la loro posizione è fissa perché dipende dalla scelta di una determinata unità di misura. 

In questa seconda parte si affronta il mondo dei numeri razionali collocati su una retta realizzata attraverso un artefatto in cui l’unità di misura è facilmente variabile, in modo da mediare il concetto di densità dell’insieme Q in R (o meglio di Q⁺ in R⁺). Tale artefatto, il “filo”, è un filo di nylon spesso, le cui estremità vengono fissate alle pareti dell’aula, oppure può essere sostituito da un bastone di una tenda da appendere alla lavagna o ad una parete. Esso rappresenta fisicamente la retta dei numeri, su cui vengono appesi dei cartoncini che riportano i numeri naturali, le unità frazionarie, le frazioni. 

Una caratteristica molto interessante del filo, rispetto alla retta disegnata sul quaderno, è la sua dinamicità: facendo scorrere i cartoncini lungo il filo si può far variare l’unità di misura. 

L’insegnante può utilizzare i cartoncini con le frazioni forniti in allegato al libro Frazioni sul Filo, costruirne personalmente con del cartoncino oppure predisporre il materiale perché vengano creati in classe dagli studenti stessi (ad esempio ciascuno crea un cartoncino con una frazione a sua scelta)¹.

Gli studenti vengono chiamati, uno ad uno, a pescare un cartoncino tra tutti quelli creati e a posizionarlo sul filo nella posizione corretta. Come indicazione per l'insegnante si tenga presente che la richiesta diventa via via più complessa mano a mano che il filo si sarà popolato di cartoncini. Almeno le prime volte potrebbe essere ragionevole lasciare per ultimi gli studenti che hanno dimostrato di aver meglio familiarizzato con tutti i concetti del percorso.

 

Cosa aspettarsi

Lo studente che per primo deve posizionare la frazione sul filo è costretto a decidere l’unità di misura, costituita dall’intervallo [0,1]. È necessario quindi posizionare subito il cartoncino con l’unità: nelle foto sottostanti lo zero è identificato con l’estremo sinistro del palo e l’1 è rappresentato rispettivamente da 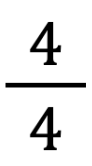  e  . 

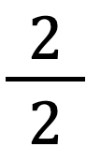Gli studenti che devono posizionare le successive frazioni si trovano di fronte a due questioni:

• Considerata l’unità di misura scelta, la frazione che devo posizionare “ci sta” sul filo? Se così non fosse si è costretti a variare l’unità di misura. Potrebbe essere necessario diminuirla per fare spazio a frazioni più grandi di 1, di 2 o di 3…oppure aumentarla per allargare lo spazio, ad esempio, tra 0 e 1 in modo da fare posto al nuovo cartoncino.
• Decidere dove posizionare il cartoncino, confrontandolo con quelli già presenti. L’insegnante chiede allo studente di rendere esplicito il ragionamento attraverso cui effettua questo confronto, e lo riporta alla lavagna.

La possibilità di aumentare dinamicamente il numero di frazioni comprese tra 0 e 1 è un’esperienza percettiva molto forte che consente di costruire il significato di densità dei numeri in Q.

Sul filo viene meno invece l’evidenza dell’unità di misura: la frazione assume il ruolo di un numero astratto e non fa più riferimento a un modello concreto, come una parte di striscia o di tovaglietta. La posizione del numero razionale sul filo è solo approssimativa: non potendo determinare in modo preciso la posizione, l’attenzione è posta prevalentemente sull’ordinamento numerico. Le frazioni equivalenti sono appese una sotto l’altra, mediando in questo modo il significato di “classe di equivalenza”, già emerso nelle fasi precedenti del percorso: un numero razionale rappresenta un insieme (potenzialmente infinito) di frazioni equivalenti alla capoclasse.

Questa attività permette agli studenti di far riferimento e quindi di utilizzare e collegare tra loro i vari significati matematici costruiti durante il percorso. 

È importante che l’insegnante raccolga alla lavagna tutti i metodi di confronto che emergono man mano che gli studenti appendono le frazioni sul filo in modo da costruire una sorta di raccolta di strategie possibili: confronto rispetto agli interi o alla metà, scomposizione in somma di interi e/o unità frazionarie, confronto delle frazioni complementari, passaggio a frazioni equivalenti con lo stesso denominatore, ….

Per esempio, da una delle classi sperimentali:

 

 

Gli studenti, per operare i confronti, mettono in pratica la capacità di stima e la familiarità con le frazioni che hanno sviluppato durante tutto il percorso. 

Ad esempio, come si può osservare nella foto della lavagna sottostante, l’argomentazione a supporto della scelta di posizionare 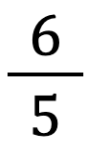  tra 1 e 2 è perché  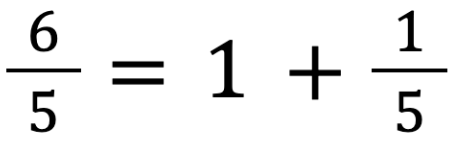(quindi >1) ma deve stare prima di  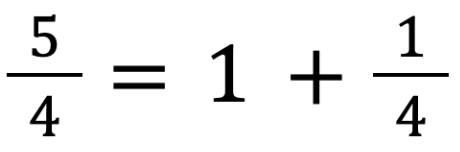perché .

 

 

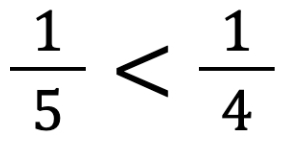È consigliabile ripetere questa attività più volte durante diverse lezioni. Gli studenti diventano via via più sicuri ed esperti nel posizionare i cartoncini sul filo, prendendo sempre più confidenza con le varie strategie di confronto. Di conseguenza l’attività si svolge più velocemente e il filo a fine lezione è più popoloso, richiedendo così confronti via via sempre più complessi. 

Nelle classi sperimentali questa attività è stata molto apprezzata dagli studenti che hanno dimostrato davvero tutti di aver acquisito una grande familiarità nella gestione delle frazioni ed erano gli studenti stessi a richiedere di “giocare” con le frazioni sul filo.

 

¹ I cartoncini in allegato al libro sono colorati in base alle varie unità frazionarie. Alla scuola secondaria di primo grado è consigliato non porre l’attenzione sui diversi colori: se non lo farà l’insegnante non lo faranno nemmeno gli studenti. File di supporto per la costruzione di cartoncini:  ⤓ Scarica Cartoncini da ritagliare

 

 

Vai all'Attività 4 ➜

 

2018_3_1011_IP.01 “LE NUOVE FRONTIERE DEL DIRITTO ALL’ISTRUZIONE. Rimuovere le difficoltà d’apprendimento, favorire una scuola inclusiva e preparare i cittadini responsabili e attivi del futuro - Fase 2". Questa iniziativa è realizzata nell'ambito del Programma operativo FSE 2014 – 2020 della Provincia autonoma di Trento grazie al sostegno finanziario del Fondo sociale europeo, dello Stato italiano e della Provincia autonoma di Trento. La Commissione europea e la Provincia autonoma di Trento declinano ogni responsabilità sull’uso che potrà essere fatto delle informazioni contenute nei presenti materiali.