Didattica della Matematica Inclusiva
nella scuola secondaria di primo grado
ATTIVITÀ 4
Un obiettivo di questo percorso è estendere la concezione di “numero” a partire dal modello primitivo di numero naturale che si è sedimentato negli studenti già dai primi anni di vita. I numeri razionali, infatti, sono caratterizzati da proprietà diverse rispetto ai numeri naturali. Ad esempio, in questo insieme numerico perdono di significato il concetto di precedente e successivo perché, tra due numeri razionali, ci sono infiniti numeri razionali. Questa caratteristica è nota come densità dell’insieme Q in R.
Una volta che gli studenti sono diventati sicuri e abili con il posizionamento delle frazioni sul filo, l’insegnante chiede loro di trovare tre frazioni diverse comprese, ad esempio, tra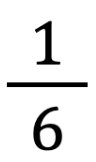 
e . Si possono scegliere due frazioni qualsiasi appese al filo ma, almeno le prime volte, consigliamo di prendere due unità frazionarie per semplicità. Dopo aver lasciato il tempo necessario affinché ognuno possa riflettere individualmente, si avvia la discussione di classe.
Cosa aspettarsi
La consegna non è assolutamente semplice e, una risposta completa, richiede una discussione lunga durante la quale i significati emergono piano piano sotto la guida attenta dell’insegnante.
Solitamente la quasi totalità della classe individua almeno una frazione compresa tra 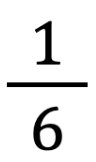e , che ovviamente è
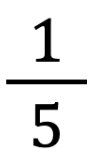. Le cose poi si complicano e alcuni studenti potrebbero essere convinti che non ci siano altre frazioni comprese tra le due unità frazionarie iniziali, oltre quella individuata.
Da un’altra classe sperimentale:
La potenzialità dell’artefatto filo, che permette di variare dinamicamente l’unità di misura di riferimento, ha aiutato gli studenti a interiorizzare, con un approccio percettivo e dinamico, la densità di Q.
Nelle classi sperimentali hanno parlato spesso di questa proprietà in termini di “fare lo zoom”, descrivendo con questa metafora la necessità di dover allargare l’unità di misura per trovare dei numeri razionali compresi tra due frazioni. In particolare, gli studenti procedono costruendo frazioni equivalenti a quelle date, con denominatore un multiplo comune tra i loro denominatori e questo processo consente loro di “fare lo zoom” per trovare delle frazioni appartenenti all’intervallo considerato.
Il concetto di numero razionale come classe di equivalenza, ovvero come un insieme infinito di frazioni equivalenti alla frazione ridotta ai minimi termini, ha permesso agli studenti di intuire che questo processo può continuare all’infinito e quindi che tra due qualsiasi numeri razionali ci sono infiniti numeri razionali.
2018_3_1011_IP.01 “LE NUOVE FRONTIERE DEL DIRITTO ALL’ISTRUZIONE. Rimuovere le difficoltà d’apprendimento, favorire una scuola inclusiva e preparare i cittadini responsabili e attivi del futuro - Fase 2". Questa iniziativa è realizzata nell'ambito del Programma operativo FSE 2014 – 2020 della Provincia autonoma di Trento grazie al sostegno finanziario del Fondo sociale europeo, dello Stato italiano e della Provincia autonoma di Trento. La Commissione europea e la Provincia autonoma di Trento declinano ogni responsabilità sull’uso che potrà essere fatto delle informazioni contenute nei presenti materiali.