
Didattica della Matematica Inclusiva
nella scuola secondaria di primo grado
ATTIVITÀ 1
Si riportano alcuni spunti possibili per lanciare la discussione in classe sul primo aspetto che vogliamo trattare in questa fase: “qual è il ruolo del resto?”
Le possibili riflessioni degli studenti a cui l’insegnante potrebbe agganciarsi per intavolare una discussione sono domande tipo “ma non basta mettere il resto nel risultato dopo la virgola?” o eventuali conflitti cognitivi di coloro che pensano che il resto coincida con le cifre decimali del quoziente ma poi si trovano di fronte ad un’evidenza diversa.
Due esempi di lancio di discussione da parte dell’insegnante:
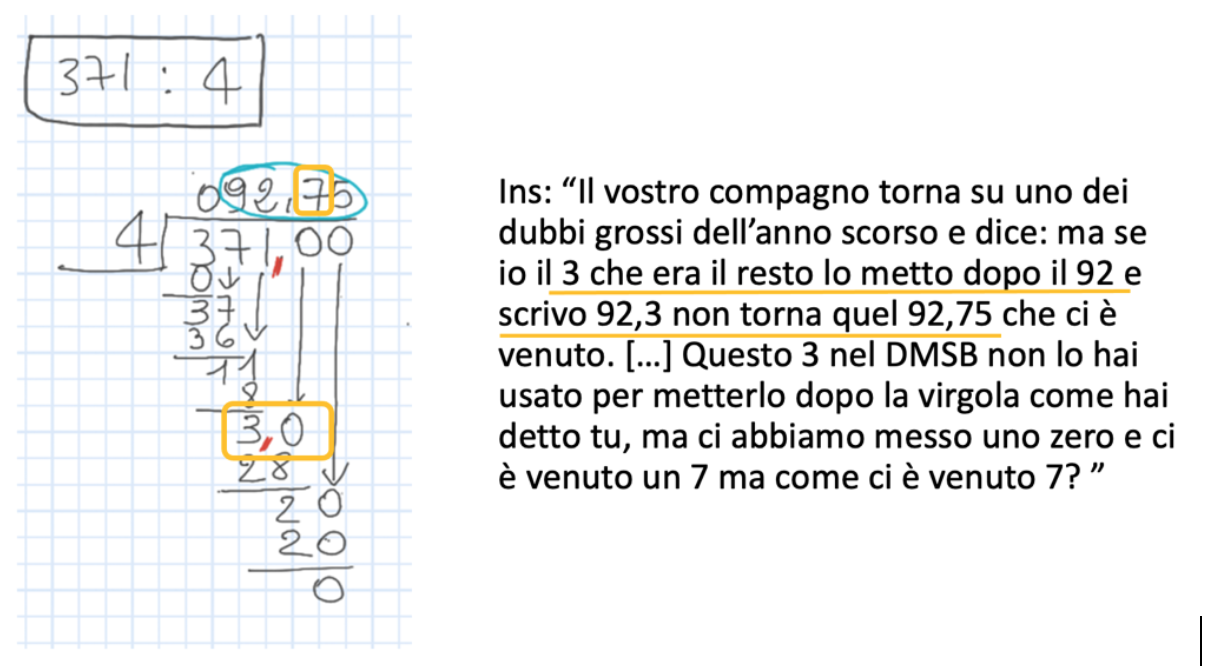
L’insegnante riporta alla classe le parole di uno studente che nello svolgere la divisione in colonna
ha ottenuto un risultato diverso rispetto alle aspettative.

L’insegnante apre il dibattito alla classe, mostrando i due diversi valori di 222 : 8 trovati da due studenti
che hanno svolto la divisione con l’algoritmo canadese.
Indicazioni per il docente
L’insegnante può lanciare la discussione sfruttando le parole o le produzioni degli studenti. In particolare, sottolinea o cerca di innescare un conflitto cognitivo in coloro che credevano che il resto corrispondesse alle cifre decimali del quoziente ponendoli di fronte ad un’evidenza diversa.
L’insegnante favorisce la discussione tra studenti, spronandoli ad argomentare e supportare le loro idee. Riprende alcune espressioni utilizzate dagli studenti, vari dubbi e riflessioni che vengono poste, cercando di portare il focus di tutta la classe sui seguenti obiettivi:
-
prendere consapevolezza che il resto contribuisce alle cifre decimali del quoziente, ma non coincide con esse;
-
comprendere che le cifre decimali del quoziente sono generate continuando a dividere il resto per il divisore.
Cosa aspettarsi
Gli studenti incontreranno delle difficoltà nel cercare di capire come poter trovare le cifre decimali del quoziente. Dalla letteratura è noto che la scrittura 222 : 8 = 27 R6, comunemente usata alla scuola primaria, ha tra le altre ricadute didattiche la trasformazione da parte degli studenti della R in “+” oppure “,”. (Si rimanda alla pagina Fase 0 del confronto di algoritmi in N per un approfondimento sulla scrittura matematica del risultato di una divisione in N che noi promuoviamo).
Per esempio, durante la discussione nella classe sperimentale in cui si è posto il problema riportato nella figura sopra, diversi studenti sostenevano che fosse corretta la scrittura 222 : 8 = 27,6 perché quello 0,75 non avrebbero saputo dove trovarlo nell’algoritmo. Alcuni studenti hanno però osservato che se avessero voluto continuare la divisione avrebbero dovuto fare il resto, cioè 6, diviso il divisore, cioè 8. Questo passaggio si è rivelato chiave perché poi è emerso che 6 : 8 = 0,75.
Discussioni analoghe sono avvenute anche nelle altre classi, talvolta anche a partire dalla divisione svolta con l’algoritmo in colonna.
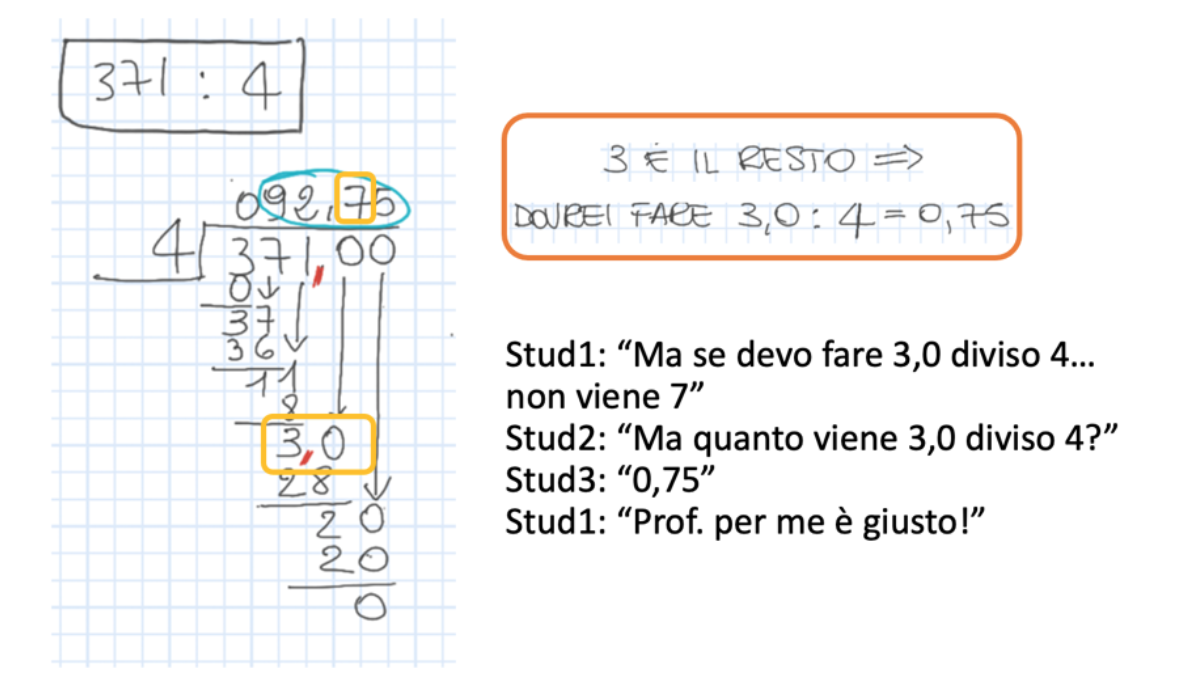
Esempio di dubbio e relativa discussione in una classe sperimentale.

Da una discussione in una classe sperimentale.
2018_3_1011_IP.01 “LE NUOVE FRONTIERE DEL DIRITTO ALL’ISTRUZIONE. Rimuovere le difficoltà d’apprendimento, favorire una scuola inclusiva e preparare i cittadini responsabili e attivi del futuro - Fase 2". Questa iniziativa è realizzata nell'ambito del Programma operativo FSE 2014 – 2020 della Provincia autonoma di Trento grazie al sostegno finanziario del Fondo sociale europeo, dello Stato italiano e della Provincia autonoma di Trento. La Commissione europea e la Provincia autonoma di Trento declinano ogni responsabilità sull’uso che potrà essere fatto delle informazioni contenute nei presenti materiali.

