
Didattica della Matematica Inclusiva
nella scuola secondaria di primo grado
MUOVERE LA GEOMETRIA > FASE 3 > ATTIVITÀ 1 > PROPOSTE DI CONSOLIDAMENTO > ATTIVITÀ 2
ATTIVITÀ 2
Di seguito riportiamo alcune attività per ragionare sulle relazioni che intercorrono tra i vari quadrilateri, che sono articolate nei seguenti file GeoGebra:
Indicazioni per il docente
Analizziamo la consegna del file “Dal parallelogramma al rettangolo non quadrato”. La consegna è riportata direttamente all’interno del file GeoGebra.

Le tre figure sotto mostrano possibili posizioni per il punto rosso; la terza figura mostra l’esito di un trascinamento in cui si è cercato di mantenere invariata (in modo instabile) la proprietà “il quadrilatero è un rettangolo”.
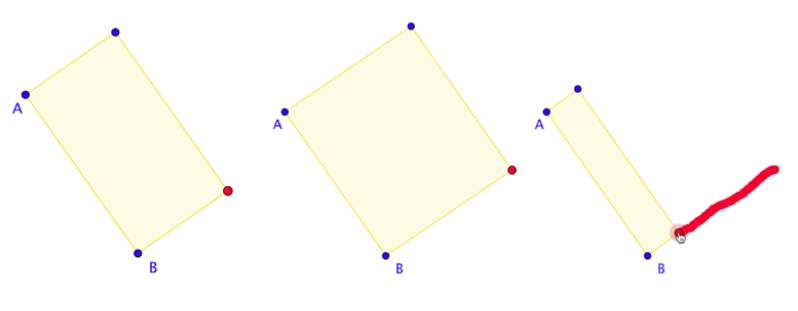
Notiamo che la presenza di “affinché” nella consegna spesso produce la ricerca di cause o condizioni di cui la proprietà che segue “affinché” è una conseguenza. Nel caso della terza figura, la traccia consente di inferire, per induzione, una proprietà che potrebbe essere condizione sufficiente da aggiungere alle proprietà di costruzione per ottenere la proprietà “il quadrilatero è un rettangolo”. In questo caso la proprietà potrebbe essere “il punto rosso appartiene alla perpendicolare ad AB per B”. Una congettura espressa in forma di enunciato condizionale su questo potrebbe essere: “Data la costruzione del parallelogramma, se il vertice rosso appartiene alla perpendicolare per B ad AB (o se l’angolo in B è retto), allora il parallelogramma è un rettangolo.”
Come altro esempio dell’utilità dello strumento traccia, pensiamo al caso del rombo (Dal parallelogramma al rombo). Si chiede di trascinare il punto rosso affinché il quadrilatero (che è un parallelogramma robusto) sia un rombo; e nel caso in cui sia possibile, dire quale proprietà deve avere il punto rosso. Se si cerca di mantenere la proprietà “il quadrilatero è un rombo” durante un trascinamento continuo (chiamato anche trascinamento di mantenimento) si può decidere di attivare lo strumento traccia per inferire regolarità nel movimento. Se, per esempio, si attiva traccia sul punto d’intersezione delle diagonali, si può notare che affinché il quadrilatero sia un rombo, questo punto deve appartenere alla circonferenza di diametro AB. La congettura “Se il punto d’intersezione delle diagonali appartiene alla circonferenza di diametro AB, allora il quadrilatero della costruzione è un rombo” è in effetti dimostrabile immediatamente, ricordando il teorema per cui ogni triangolo inscritto in una semicirconferenza è rettangolo nell’angolo opposto al lato che coincide con il diametro della semicirconferenza.

Non ci aspettiamo che gli studenti arrivino a formulare questo tipo di congetture, ma riteniamo che sia importante che i docenti siano consapevoli anche di queste potenzialità del software, per poter continuare ad offrire attività adatte a diversi profili di apprendimento matematico in una stessa classe. In generale, riteniamo che ottime attività esplorative per la classe siano attività descritte metaforicamente come aventi “soglia bassa e soffitto alto” in modo che tutti gli studenti possano trovare punti d’entrata per incuriosirsi e partecipare, rimanendo stimolati.
Cosa aspettarsi
Questo tipo di richieste sono sicuramente attività più complesse e non sono gestibili dagli studenti in autonomia. È importante quindi proporle in classe affinché sia l’insegnante ad orchestrare la discussione, rallentandola qualora fosse necessario e invitando magari ad attivare la traccia in punti opportuni che permettano di rendere più visibile la congettura di qualche studente.
È possibile utilizzare i file dopo aver analizzato le proprietà di tutti i quadrilateri, come attività conclusiva e di riepilogo, ma anche stimolare la riflessione già di volta in volta attraverso i file dell’attività 1 con domande del tipo:
-
Quali proprietà mancano al rombo per essere un quadrato?
-
Quali proprietà mancano al rettangolo per essere un quadrato?
-
Quali proprietà mancano al parallelogramma per essere un rombo?
-
Quali proprietà mancano al parallelogramma per essere un rettangolo?
-
Quali proprietà mancano al parallelogramma per essere un quadrato?
Saranno gli studenti a scegliere di volta in volta da quale figura dinamica partire per cercare di spiegare la loro congettura. Può essere utile che poi l’insegnante riporti in alcune slide da lasciare agli studenti, uno screenshot del file GeoGebra con il movimento visualizzato da quella classe a giustificazione della loro congettura.

Nelle classi sperimentali ci siamo accorti come sia proprio l’immagine mentale dei movimenti delle figure dinamiche ad essere richiamata dagli studenti per rispondere a domande simili anche in momenti successivi.
Nella seconda domanda contenuta nei file presentati in questa attività 2, si prova a far fare agli studenti un salto ulteriore in quanto viene chiesto loro di cercare di mantenere invariata una determinata proprietà: “Nel caso sia possibile, quale proprietà deve avere il punto rosso?”.
Come già accennato nella sezione Indicazioni per il docente, non ci aspettiamo che gli studenti arrivino a dare una risposta formalmente corretta da un punto di vista dei teoremi della geometria euclidea, ma pensiamo che questo tipo di domande siano ottimi spunti per alzare il livello della discussione se l’insegnante lo ritenesse opportuno o possibili approfondimenti da lasciare agli studenti più coinvolti e stimolati.
Dall’altra parte, anche gli studenti più deboli saranno spesso invogliati a provare a muovere il punto rosso e cercare visivamente conferma ai loro movimenti, sentendosi quindi coinvolti nell’attività.
2018_3_1011_IP.01 “LE NUOVE FRONTIERE DEL DIRITTO ALL’ISTRUZIONE. Rimuovere le difficoltà d’apprendimento, favorire una scuola inclusiva e preparare i cittadini responsabili e attivi del futuro - Fase 2". Questa iniziativa è realizzata nell'ambito del Programma operativo FSE 2014 – 2020 della Provincia autonoma di Trento grazie al sostegno finanziario del Fondo sociale europeo, dello Stato italiano e della Provincia autonoma di Trento. La Commissione europea e la Provincia autonoma di Trento declinano ogni responsabilità sull’uso che potrà essere fatto delle informazioni contenute nei presenti materiali.

