FRAZIONI SUL FILO > FASE 2 > ATTIVITÀ 1

 

ATTIVITÀ 1

 

L’insegnante guida il passaggio da tovaglietta a striscia, che si realizza accostando tra loro vari rettangoli di dimensione 2x16 quadretti. Si considera adesso come unità di misura un rettangolo più lungo e schiacciato e, riportandolo varie volte sul quaderno, si forma una striscia alta due quadretti in cui riportare l’unità di misura tante volte quante lo permette la lunghezza della striscia stessa, segnando così i numeri naturali 0, 1, 2, 3…

A questo punto l’insegnante lascia il tempo agli studenti di costruire le varie strisce sul proprio quaderno e di segnare su ognuna una delle unità frazionarie indicate: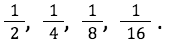 

L’insegnante poi disegna le strisce alla lavagna o proietta un file GeoGebra precedentemente costruito, tipo il seguente:

 

Cosa aspettarsi

Durante l’attività di costruzione di questa pagina di quaderno, gli studenti sviluppano spontaneamente ragionamenti di confronto e ordinamento che danno origine alle prime discussioni. 

Il confronto tra le diverse unità frazionarie risulta percettivamente evidente dalle strisce disegnate sul quaderno una sotto l’altra e allineate a sinistra in corrispondenza dello zero.

Per esempio, si può osservare la relazione che sussiste tra l’ordinamento delle unità frazionarie e la grandezza del denominatore: più il denominatore è grande e più l’unità frazionaria è piccola (quindi più vicina allo zero).  Dalla rappresentazione appaiono evidenti anche i rapporti tra unità frazionarie: ad esempio tra ema anche tra e.

Tali osservazioni potrebbero essere già emerse durante le attività con la tovaglietta e in questa fase vengono ulteriormente consolidate.

 

Sempre dal confronto tra le varie strisce appositamente costruite una sotto l’altra, emerge anche il concetto di frazioni equivalenti, ovvero frazioni che sono alla stessa distanza dallo zero. A tale concetto è importante dedicare parte della discussione e, in particolare, vale la pena portare l’attenzione sul significato di frazione ridotta ai minimi termini come rappresentate della classe di frazioni equivalenti.

In questa discussione sulle frazioni equivalenti occorre prestare attenzione che gli studenti non sviluppino l’automatismo per cui si convincono che due frazioni sono equivalenti se o solo se esiste un numero naturale per cui moltiplicare o dividere il numeratore e il denominatore della prima frazione per ottenere la seconda. Come sottolineano Di Martino e Zan (2019), tale procedura permette infatti di trovare frazioni equivalenti a partire da una frazione data, ma non permette di trovarle tutte (ovvero è condizione necessaria ma non sufficiente). Un semplice esempio basta a dimostrare che tale definizione è scorretta: 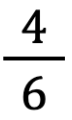  e 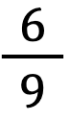 sono equivalenti ma non si possono ottenere moltiplicando o dividendo numeratore e denominatore per un numero naturale n. Gli stessi autori invitano a prestare particolare attenzione per evitare che la definizione diventi la descrizione di un comportamento da seguire:

«In definitiva la “regola” dice come trovare una frazione equivalente a una data, ma non come riconoscere due frazioni tra loro equivalenti, che è un aspetto molto più significativo dal punto di vista matematico. Tale “regola” […] rischia di sostituirsi alla definizione, creando una definizione implicita erronea di frazioni equivalenti » (Di Martino & Zan, 2019, p. 68).

 

 

Vai all'Attività 2 ➜

 

2018_3_1011_IP.01 “LE NUOVE FRONTIERE DEL DIRITTO ALL’ISTRUZIONE. Rimuovere le difficoltà d’apprendimento, favorire una scuola inclusiva e preparare i cittadini responsabili e attivi del futuro - Fase 2". Questa iniziativa è realizzata nell'ambito del Programma operativo FSE 2014 – 2020 della Provincia autonoma di Trento grazie al sostegno finanziario del Fondo sociale europeo, dello Stato italiano e della Provincia autonoma di Trento. La Commissione europea e la Provincia autonoma di Trento declinano ogni responsabilità sull’uso che potrà essere fatto delle informazioni contenute nei presenti materiali.