I PROBLEMI > FASE 4 > ATTIVITÀ 1

 

ATTIVITÀ 1

La consegna propone due situazioni problematiche per le quali può essere fatta esattamente la stessa rappresentazione e viene fornita agli studenti chiedendo loro di svolgere e confrontare i due problemi. 

 

 

⤓ Clicca qui per scaricare  

 

Indicazioni per il docente

L’insegnante concede il tempo necessario affinché ciascuno studente rifletta autonomamente sulla consegna, passa tra i banchi e osserva quali sono i ragionamenti e le rappresentazioni adottati da ognuno. Gli studenti faranno sicuramente molte domande, tuttavia è importante cercare di non rispondere in maniera troppo esplicita alle varie richieste di suggerimenti ma, per esempio, riformulare la consegna o il testo dei problemi con parole più semplici per renderlo maggiormente comprensibile. 

Si è scelto di assegnare un problema in cui i soggetti fossero i “segmenti” invece che i “numeri” per vedere se qualche studente fosse invogliato a rappresentare usando segmenti, invece che palline. Nel caso come questo, in cui entrano in gioco relazioni di tipo frazionario può, infatti, risultare utile fare un segmento di lunghezza arbitraria e poi suddividerlo in parti uguali. Questo aspetto, se emergesse in qualche modo dagli studenti, può essere ripreso dall’insegnante durante la discussione, riportando alla lavagna il segmento e sottolineando come non ci sia la necessità di tracciarlo di una lunghezza specifica individuata, ad esempio, da un determinato numero di quadretti.

 

Per i due problemi proposti possono essere fatte, rispettivamente, le seguenti rappresentazioni:

 

        

 

Si tratta di fatto esattamente della stessa rappresentazione, a meno di scambiare l’ordine delle prime due righe.

La differenza che si vuole cercare di far emergere durante la discussione e sulla quale soffermarsi è:

• nel primo caso una pallina rappresenta un’unità frazionaria;

• nel secondo caso una pallina rappresenta l’intero.

 

Riassumendo, gli obiettivi principali della discussione sono:

• discutere come identificare «l’intero di riferimento»;

• far emergere il significato della pallina quando rappresenta un’unità frazionaria;

• far emergere diverse rappresentazioni che corrispondono a diversi ragionamenti;

• abituare gli studenti a spiegare e ad argomentare il proprio ragionamento.

 

Cosa aspettarsi

A questo punto del percorso tutti gli studenti avranno familiarizzato con l’uso delle rappresentazioni e proveranno a costruirne una per risolvere questi problemi. 

Nelle classi sperimentali questa volta il 30-40% degli studenti, probabilmente invogliati dal testo del problema, ha utilizzato i segmenti nella rappresentazione ma comunque abbiamo osservato che li ha poi gestiti quasi come se fossero palline. Infatti, sono stati principalmente disegnati segmenti lunghi o 3 o 6 quadretti e non segmenti di lunghezza arbitraria su cui poi agire operando delle suddivisioni in parti uguali in base al testo del problema.

La cosa bella, che merita di essere sottolineata, è che gli studenti hanno discusso tra loro sulla rappresentazione più efficace e più significativa, a dimostrazione dell’importanza che ha acquisito nel loro processo di pensiero. In particolare, hanno confrontato l’uso dei segmenti o delle palline osservando che il segmento come “intero di riferimento” è più utile perché può essere comodamente suddiviso per ottenere 1/3, invece con la pallina la suddivisone in tre parti uguali è scomoda. Tuttavia hanno anche notato che, se per tracciare il segmento ci si basa sui quadretti, vuol dire che si è già pensato prima a quanti quadretti usare per rappresentare l’intero e questo ragionamento equivale a quello usato per le palline. 

La maggior parte degli studenti ha quindi preferito la rappresentazione con le palline e c’è stato qualcuno che inizialmente ha disegnato una pallina per rappresentare 1/3 ma poi si è bloccato non riuscendo a capire quante palline utilizzare per rappresentare il secondo segmento. L’insegnante ha quindi chiesto a questi studenti perché per 1/3 avessero disegnato 1 pallina e questa semplice domanda è bastata loro per realizzare che l’altro segmento dovesse essere 3 palline, e hanno risposto “perché 1/3 vuol dire 1 di 3”.

In generale, in tutte le classi, da un primo giro di idee, gli studenti hanno detto che i due problemi di fatto erano uguali e che questo si può vedere dalla rappresentazione che è la stessa in entrambi i casi. Hanno argomentato che sono la stessa cosa 

“perché 1/3 e triplo sono due facce della stessa medaglia”

Il fatto di scambiare l’ordine delle righe nella rappresentazione è stato oggetto di discussione ma hanno concluso che è una cosa che si può sempre fare 

“perché dipende da dove si sceglie di cominciare”

“perché non ti dice mica primo segmento, secondo segmento…”

Per far nascere negli studenti il dubbio e avviare la discussione è stato fondamentale avere la terza rappresentazione, quella in basso nella lavagna di sinistra (vedi foto), proposta in ogni classe sperimentale da un solo studente. Nel caso non dovesse emergere nella propria classe, suggeriamo all’insegnante di proporla per lanciare la discussione, per esempio dicendo “nell’altra classe/l’anno scorso qualcuno ha detto che si può anche fare così…”

 

 

Nell’immagine è riportata la foto di una lavagna, in cui ci sono alcune cose scritte in rosso dall’insegnante e sono quelle emerse durante la discussione, mentre quelle scritte in blu sono le proposte iniziali degli studenti. 

Grazie alla terza rappresentazione (in basso a sinistra nell’immagine) gli studenti si sono resi conto che, anche se le rappresentazioni dei due problemi con le palline sembrano uguali, in realtà non è così. L’aspetto cruciale da discutere è quindi come identificare «l’intero di riferimento».

Per evidenziare meglio questa differenza gli studenti hanno proposto di scrivere n; 3n; 4n accanto alle palline nella rappresentazione del secondo problema e poi hanno detto che nel primo problema “3 palline è n” e di conseguenza “1 pallina ” e “4 palline ”.

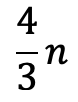In alternativa c’è stato anche chi ha proposto di inserire nelle due rappresentazioni rispettivamente 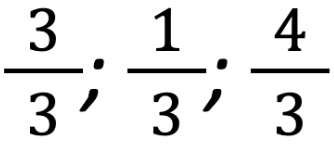  e uno; triplo; quadruplo.

Per concludere, il disegno della pallina suddivisa come nella terza rappresentazione è stato utile, anzi fondamentale, per il confronto delle due situazioni problematiche, perché l’intero è rappresentato da una pallina, esattamente come nel secondo caso. Tuttavia, secondo gli studenti quella rappresentazione è scomoda 

“... perché devi dividere la pallina in 3 pezzi e poi lavorare con i pezzi”

 

Vai all'Attività 2 ➜

 

2018_3_1011_IP.01 “LE NUOVE FRONTIERE DEL DIRITTO ALL’ISTRUZIONE. Rimuovere le difficoltà d’apprendimento, favorire una scuola inclusiva e preparare i cittadini responsabili e attivi del futuro - Fase 2". Questa iniziativa è realizzata nell'ambito del Programma operativo FSE 2014 – 2020 della Provincia autonoma di Trento grazie al sostegno finanziario del Fondo sociale europeo, dello Stato italiano e della Provincia autonoma di Trento. La Commissione europea e la Provincia autonoma di Trento declinano ogni responsabilità sull’uso che potrà essere fatto delle informazioni contenute nei presenti materiali.