MUOVERE LA GEOMETRIA > FASE 1 > ATTIVITÀ 1 > ATTIVITÀ 2

 

ATTIVITÀ 2

L’insegnante lancia una discussione sull’idea di altezza che hanno gli studenti, stando volutamente molto vaga nella formulazione dell’input proposto.

Per esempio:

Indicazioni per il docente

Come accennato precedentemente, riteniamo molto importante aprire il percorso facendo una riflessione con gli studenti sull’uso della parola altezza in matematica e nella vita di tutti i giorni. Si possono fare diversi esempi (altezza di una persona, altezza di una montagna, altezza di un oggetto, altezza di un figura geometrica…) e arrivare alla conclusione che ci sono vari modi possibili di definire l’altezza. L’importante conquista e presa di consapevolezza da parte degli studenti dovrebbe essere che, in contesti diversi, una definizione può essere più efficace di un’altra, in particolare noi saremo interessati a capire qual è la definizione che viene utilizzata in matematica e perché.

È importante che, in questo contesto di discussione iniziale, l’insegnante valorizzi le considerazioni di tutti gli studenti senza mai giudicarne la correttezza o esprimere giudizi. Può invece cercare di evidenziare eventuali analogie o differenze tra le proposte di studenti differenti per favorire la discussione e il confronto.

Al termine della discussione (vedi la prossima sezione “Cosa Aspettarsi”) dovrebbero essere emerse spontaneamente diverse definizioni di altezza. L’insegnante può allora provare a formalizzare e riassumere alla lavagna o in una slide. Per esempio, di seguito è riportata una slide realizzata sulla base delle osservazioni emerse in una classe sperimentale:

 

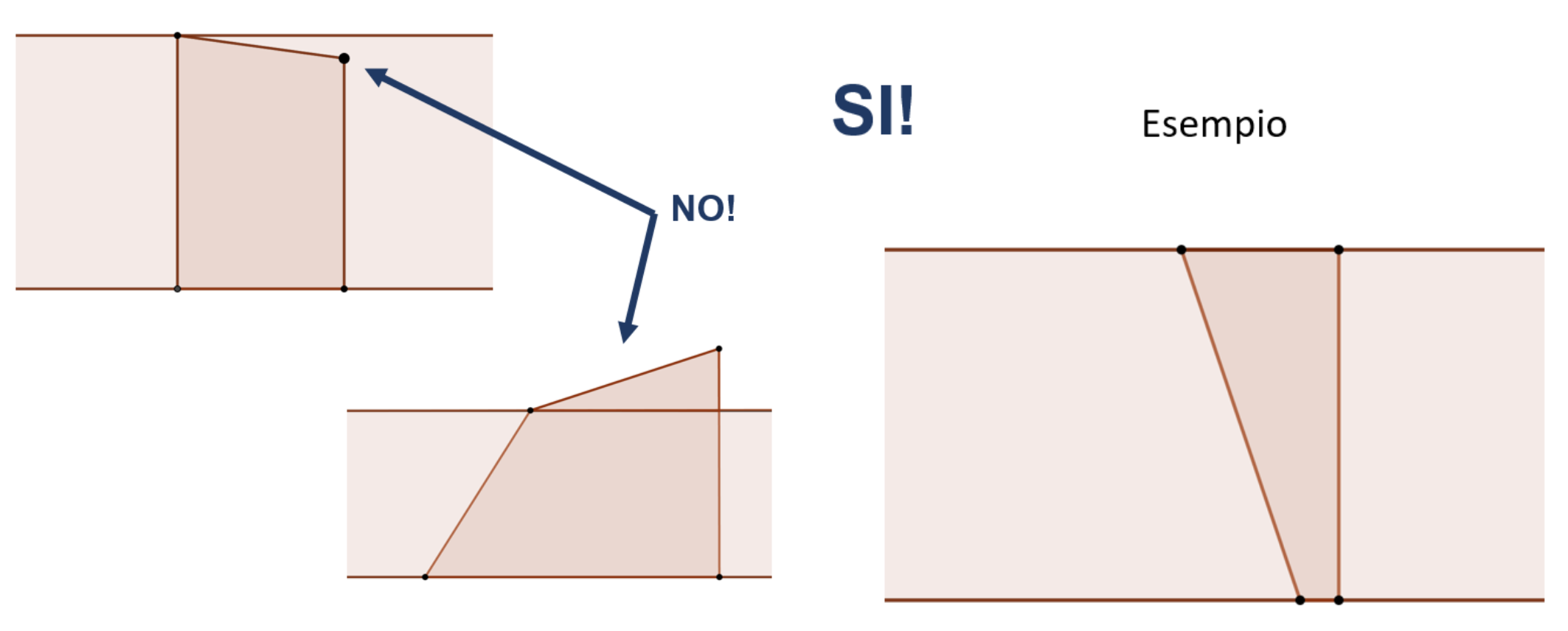
È possibile che in questa fase del percorso non sia ancora opportuno introdurre il concetto di “famiglia di tutti i segmenti che individuano l’altezza della striscia”, se non emerso durante la discussione. In tal caso si può parlare del “segmento che individua l’altezza della striscia” per andare a perfezionare la definizione durante la Fase 3 in cui i file di GeoGebra, con la relativa funzione di trascinamento, permetteranno di capire meglio il concetto di altezza come rappresentante di una famiglia di segmenti. 

 

Cosa aspettarsi

Come riportato anche nei numerosi studi della letteratura in didattica della matematica, gli studenti parleranno moltissimo di altezza come di una quantità fortemente legata alla gravità, a una direzione «orizzontale» e una «verticale», «dall’alto verso il basso» o viceversa, di «lunghezza verticale», «lunghezza da una base ad un punto sopra» e accompagneranno le loro affermazioni con gesti delle braccia che rispecchiano queste due direzioni.

Spesso un esempio molto usato è quello dell’altezza di una persona, che gli studenti definiscono come la misura “dal piede fino alla testa”, “dal pavimento alla testa”. La cosa interessante che si può fare è chiedere poi ad un ragazzo di stendersi a terra e ai compagni di misurare la sua altezza. Nelle classi sperimentali si è aperta una bella discussione: per alcuni l’altezza rimaneva invariata, per altri ora era “dalla schiena alla pancia”, per altri ancora “dipende dal punto di osservazione”. Addirittura alcuni si sono spinti a dire che a livello anatomico l’altezza del compagno non poteva cambiare, mentre per la geometria sì perché in geometria è sempre “da sotto a sopra”.

 

Un’altra discussione molto interessante emersa spontaneamente dagli studenti è se ogni oggetto abbia sempre e solo UNA altezza. Per alcuni “un oggetto con due punte, ha due altezze”, per altri invece va considerata sempre solo l’altezza massima. 

Stud 1: “nel quadrato ci sono due linee dall’alto verso il basso, ma l’altezza è una sola”.

Stud 2: “nel cubo l’altezza è sempre uguale”

Stud 3: “…e se invece lo appoggi su un vertice, è più alto?”

Stud 4: “potrebbe essere che una figura abbia più di un’altezza?”

 

Infine alcuni si sono spinti a pensare che in certi casi le altezze possano essere infinite, ad esempio nel caso di una matita inclinata rispetto al piano di appoggio (e non perpendicolare ad esso):

Come si può notare dalla registrazione che riporta un breve estratto di discussione di classe, guidata dall’insegnante che interviene a più riprese lasciando però molto spazio agli studenti e orchestrando i loro interventi alla luce del suo obiettivo didattico, questi ragazzi vedevano la matita inserita in una sorta di striscia. Per misurare la matita alcuni si muovevano perpendicolarmente dal piano di appoggio al punto più alto o meglio, per il momento parlavano in termini di “verticalità” rispetto al piano di appoggio. Altri invece sostenevano che la misura andasse fatta “inclinata”, ovvero lungo l’oggetto stesso che sarebbe stato quindi sempre alto uguale, indipendentemente dalla sua inclinazione.

 

Nelle classi dove non erano emerse spontaneamente riflessioni di questo tipo, l’insegnante ha chiesto quanto è alta la torre di Pisa e subito si sono attivate considerazioni molto simili. “Al pilota che deve atterrare all’aeroporto di Pisa serve la misura dal terreno al punto più alto”, “l’ingegnere che l’aveva disegnata, aveva calcolato l’altezza obliqua”.

Un’ultima bellissima osservazione emersa da uno studente è stata: “l’altezza varia a seconda di a cosa serve”.  Questo è molto importante per predisporre poi le basi a varie possibile definizioni di altezza nella vita reale e all’interno della geometria. 

Concludiamo ricordando che l’obiettivo di queste lezioni non è dare delle risposte ma suscitare delle domande e delle riflessioni negli studenti. Serve inoltre all’insegnante a capire con quali idee di altezza deve relazionarsi e questo è molto importante per poter costruire un sapere più approfondito.

Le altezze dei quadrilateri e dei triangoli verranno poi riprese in modo specifico nelle prossime fasi, sempre alla luce di quanto emerso in queste prime lezioni.